Search any question & find its solution
Question:
Answered & Verified by Expert
The maximum value of $z=7 x+8 y$ subject to the constraints $x+y \leq 20, y \geq 5, x \leq 10, x \geq 0, y \geq 0$ is
Options:
Solution:
2584 Upvotes
Verified Answer
The correct answer is:
$160$
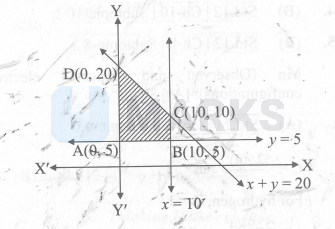
Feasible region lies on the origin side of lines $x+y=20, x=10$ and on non-origin side of $y=5$.
$\therefore \quad$ Corner points of the feasible region are $\mathrm{A}(0,5), \mathrm{B}(10,5), \mathrm{C}(10,10)$ and $\mathrm{D}(0,20)$
$\mathrm{z}$ at $\mathrm{A}(0,5)=40$
$\mathrm{z}$ at $\mathrm{B}(10,5)=110$
$\mathrm{z}$ at $\mathrm{C}(10,10)=150$
$\mathrm{z}$ at $\mathrm{D}(0,20)=160$
$\therefore \quad$ Maximum value of $\mathrm{z}$ is 160 .
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.