Search any question & find its solution
Question:
Answered & Verified by Expert
The molar conductivity of \(0.025 \mathrm{~mol} \mathrm{~L}^{-1}\) methanoic acid is \(46.1 \mathrm{~S} \mathrm{~cm}^2 \mathrm{~mol}^{-1}\). Calculate its degree of dissociation and dissociation constant. Given \(\lambda^{\circ}\left(\mathrm{H}^{+}\right)=349.6 \mathrm{~S} \mathrm{~cm}{ }^2\) \(\mathrm{mol}^{-1}\) and \(\lambda^0\left(\mathrm{HCOO}^{-}\right)=54.6 \mathrm{~S} \mathrm{~cm}^2 \mathrm{~mol}^{-1}\).
Solution:
2208 Upvotes
Verified Answer
\(\begin{aligned}
\Lambda_{\mathrm{m}}^{\mathrm{o}}(\mathrm{HCOOH}) &=\lambda^{\circ}\left(\mathrm{H}^{+}\right)+\lambda^{\circ}\left(\mathrm{HCOO}^{-}\right) \\
&=349.6+54.6 \\
&=404.2 \mathrm{~S} \mathrm{~cm}{ }^2 \mathrm{~mol}^{-1} \\
\Lambda_{\mathrm{m}}^{\mathrm{C}} &=46.1 \mathrm{~S} \mathrm{~cm}{ }^2 \mathrm{~mol}^{-1} \\
\therefore \quad \alpha &=\frac{\Lambda_{\mathrm{m}}^{\mathrm{C}}}{\Lambda_{\mathrm{m}}^{\mathrm{o}}}=\frac{46.1}{404.2}=0.114
\end{aligned}\)
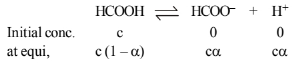
\(\therefore \quad K_a=\frac{c \alpha \cdot c \alpha}{c(1-\alpha)}=\frac{c \alpha^2}{1-\alpha}\)
\(=\frac{0.025 \times(0.114)^2}{1-0.114}\)
\(=3.67 \times 10^{-4} \mathrm{~mol} \mathrm{~L}^{-1}\)
\Lambda_{\mathrm{m}}^{\mathrm{o}}(\mathrm{HCOOH}) &=\lambda^{\circ}\left(\mathrm{H}^{+}\right)+\lambda^{\circ}\left(\mathrm{HCOO}^{-}\right) \\
&=349.6+54.6 \\
&=404.2 \mathrm{~S} \mathrm{~cm}{ }^2 \mathrm{~mol}^{-1} \\
\Lambda_{\mathrm{m}}^{\mathrm{C}} &=46.1 \mathrm{~S} \mathrm{~cm}{ }^2 \mathrm{~mol}^{-1} \\
\therefore \quad \alpha &=\frac{\Lambda_{\mathrm{m}}^{\mathrm{C}}}{\Lambda_{\mathrm{m}}^{\mathrm{o}}}=\frac{46.1}{404.2}=0.114
\end{aligned}\)
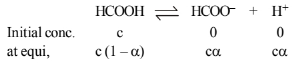
\(\therefore \quad K_a=\frac{c \alpha \cdot c \alpha}{c(1-\alpha)}=\frac{c \alpha^2}{1-\alpha}\)
\(=\frac{0.025 \times(0.114)^2}{1-0.114}\)
\(=3.67 \times 10^{-4} \mathrm{~mol} \mathrm{~L}^{-1}\)
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.