The given lines are
$x+3 y=10$
and
$6 x^2+x y-y^2=0$


$\begin{aligned} & 6 x^2+3 x y-2 x y-y^2=0 \\ & 3 x(2 x+y)-y(2 x+y)=0 \\ & 3 x-y=0 \\ & 2 x+y=0 \\ & \end{aligned}$
On solving Eqs. (i) and (ii), we get
$x+3 \cdot(3 x)=10$
$\begin{aligned} \Rightarrow & 10 x & =10 \\ \Rightarrow & x & =1\end{aligned}$
and
$\begin{array}{r}3 \cdot 1-y=0 \\ y=3\end{array}$
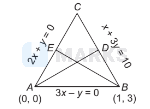
$\therefore$ Coordinates of $B$ are $(1,3)$.
On solving Eqs. (ii) and (iii), we get
$x=0, y=0$
$\therefore$ Coordinates of $A$ are $(0,0)$.
A line perpendicular to $B C$ is
$3 x-y=\lambda$
It passes through $(0,0)$, then $0-0=\lambda$
$\Rightarrow \quad \lambda=0$
The line $A D$ is $\quad 3 x-y=0$
A line perpendicular to $A C$ is
$x-2 y=\lambda$
It passes through $(1,3)$, then $1-6=\lambda$
$\lambda=-5$
The line $B E$ is
$x-2 y=-5$
On solving Fqs. (iv) and (v), we get
$x=1, y=3$
Thus, the coordinates of required orthocentre is $(1,3)$.