Search any question & find its solution
Question:
Answered & Verified by Expert
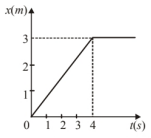
The position-time graph of a body of mass $2 \mathrm{~kg}$ is as given in figure. What is the impulse on the body at $t=0 \mathrm{~s}$ and $t=4 \mathrm{~s}$.

Solution:
2844 Upvotes
Verified Answer
As given that, mass of the body $(\mathrm{m})=2 \mathrm{~kg}$
From the position-time graph, the body is at $x=0$ when $t=0$, i.e., body is at rest so initial velocity $\left(\vec{v}_1\right)$ is zero
From $t \geq 0 \mathrm{~s}$ to $t \leq 4 \mathrm{~s}$, the slope of position-time graph is a straight line, which shows that body moves with uniform velocity.
Beyond $t \geq 4 \mathrm{~s}$, the graph is a straight line parallel to time axis, i.e. body is at rest $\left(\vec{v}_3=0\right)$.
Velocity of the body $=$ slope of position-time graph
$$
\vec{v}_2=\tan \theta=\frac{3}{4} \mathrm{~m} / \mathrm{s}=0.75 \mathrm{~m} / \mathrm{s}
$$
At $t \geq 4$ the slope of graph is zero so velocity, $\vec{v}_3=0$
$$
\begin{aligned}
\text { Impulse } &=\vec{F} \cdot t \\
&=\frac{\overrightarrow{d P}}{d t} \times \overline{d t}=\overrightarrow{d P}
\end{aligned}
$$
So, impulse $=$ change in momentum
Impulse at $(t=0)=m\left(\vec{v}_2-\vec{v}_1\right)$
$$
=2[0.75-0]=1.5 \mathrm{~kg}-\mathrm{m} / \mathrm{s}
$$
(increased)
Impulse at $(t=4)=m\left(\vec{v}_3-\vec{v}_2\right)$
$$
\begin{array}{r}
=-2(0-0.75)=-1.5 \mathrm{~kg}-\mathrm{m} / \mathrm{s} \\
\quad \text { (decreased) }
\end{array}
$$
From the position-time graph, the body is at $x=0$ when $t=0$, i.e., body is at rest so initial velocity $\left(\vec{v}_1\right)$ is zero
From $t \geq 0 \mathrm{~s}$ to $t \leq 4 \mathrm{~s}$, the slope of position-time graph is a straight line, which shows that body moves with uniform velocity.
Beyond $t \geq 4 \mathrm{~s}$, the graph is a straight line parallel to time axis, i.e. body is at rest $\left(\vec{v}_3=0\right)$.
Velocity of the body $=$ slope of position-time graph
$$
\vec{v}_2=\tan \theta=\frac{3}{4} \mathrm{~m} / \mathrm{s}=0.75 \mathrm{~m} / \mathrm{s}
$$
At $t \geq 4$ the slope of graph is zero so velocity, $\vec{v}_3=0$
$$
\begin{aligned}
\text { Impulse } &=\vec{F} \cdot t \\
&=\frac{\overrightarrow{d P}}{d t} \times \overline{d t}=\overrightarrow{d P}
\end{aligned}
$$
So, impulse $=$ change in momentum
Impulse at $(t=0)=m\left(\vec{v}_2-\vec{v}_1\right)$
$$
=2[0.75-0]=1.5 \mathrm{~kg}-\mathrm{m} / \mathrm{s}
$$
(increased)
Impulse at $(t=4)=m\left(\vec{v}_3-\vec{v}_2\right)$
$$
\begin{array}{r}
=-2(0-0.75)=-1.5 \mathrm{~kg}-\mathrm{m} / \mathrm{s} \\
\quad \text { (decreased) }
\end{array}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.