Search any question & find its solution
Question:
Answered & Verified by Expert
The probability distribution of a random variable is given below
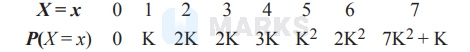
Then, $P(0 < \mathrm{x} < 5)$ is equal to
Options:
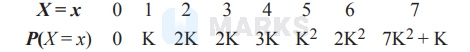
Then, $P(0 < \mathrm{x} < 5)$ is equal to
Solution:
1194 Upvotes
Verified Answer
The correct answer is:
$\frac{8}{10}$
As we know, $\sum_{i=1}^8 P\left(x_i\right)=1$
$\begin{aligned}
& 0+K+2 K+2 K+3 K+K^2+2 K^2+7 K^2+K=1 \\
& 9 K+10 K^2=1 \\
& 10 K^2+9 K-1=0 \\
& 10 K^2+10 K-K-1=0 \\
& 10 K(K+1)-1(K+1)=0 \\
& (K+1)(10 K-1)=0 \\
& \therefore \quad K=-1, \frac{1}{10}
\end{aligned}$
As the probability cannot be negative. So $\mathrm{K}$ must be greater than 0 .
$\begin{aligned}
& \therefore \quad K=\frac{1}{10} \\
& P(0 < x < 5)=P(X=1)+P(X=2) \\
& +P(X=3)+P(X=4) \\
& =K+2 K+2 K+3 K=8 K \\
& =\frac{8}{10}
\end{aligned}$
$\begin{aligned}
& 0+K+2 K+2 K+3 K+K^2+2 K^2+7 K^2+K=1 \\
& 9 K+10 K^2=1 \\
& 10 K^2+9 K-1=0 \\
& 10 K^2+10 K-K-1=0 \\
& 10 K(K+1)-1(K+1)=0 \\
& (K+1)(10 K-1)=0 \\
& \therefore \quad K=-1, \frac{1}{10}
\end{aligned}$
As the probability cannot be negative. So $\mathrm{K}$ must be greater than 0 .
$\begin{aligned}
& \therefore \quad K=\frac{1}{10} \\
& P(0 < x < 5)=P(X=1)+P(X=2) \\
& +P(X=3)+P(X=4) \\
& =K+2 K+2 K+3 K=8 K \\
& =\frac{8}{10}
\end{aligned}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.