Search any question & find its solution
Question:
Answered & Verified by Expert
The radius of a circle touching all the four circles $(x \pm \lambda)^2+(y \pm \lambda)^2=\lambda^2$ is
Options:
Solution:
2517 Upvotes
Verified Answer
The correct answer is:
$(\sqrt{2}-1) \lambda$
Clearly the required circle have circle with centre at origin
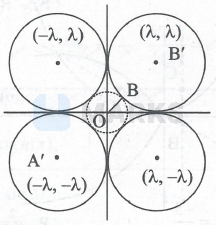
In figure, If radius of such circle $=r$ then $\mathrm{OB}=r$
$$
\begin{aligned}
& r+r+\lambda+\lambda=\mathrm{A}^{\prime} \mathrm{B}^{\prime} \\
& 2(r+\lambda)=\sqrt{(2 \lambda)^2+(2 \lambda)^2} \\
& \Rightarrow r=(\sqrt{2}-1) \lambda
\end{aligned}
$$

In figure, If radius of such circle $=r$ then $\mathrm{OB}=r$
$$
\begin{aligned}
& r+r+\lambda+\lambda=\mathrm{A}^{\prime} \mathrm{B}^{\prime} \\
& 2(r+\lambda)=\sqrt{(2 \lambda)^2+(2 \lambda)^2} \\
& \Rightarrow r=(\sqrt{2}-1) \lambda
\end{aligned}
$$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.