Search any question & find its solution
Question:
Answered & Verified by Expert
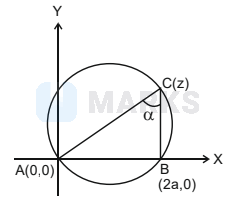
The side $A B$ of $\triangle A B C$ is fixed and is of length $2 a$ unit. The vertex moves in the plane such that the vertical angle is always constant and is $\alpha$. Let $x$-axis be along $A B$ and the origin be at $A$. Then the locus of the vertex is
Options:
Solution:
2977 Upvotes
Verified Answer
The correct answer is:
$x^2+y^2-2 a x-2 a y \cot \alpha=0$
Let, $c=z=x+i y$
$\begin{aligned}
&\arg \left(\frac{2 \mathrm{a}-\mathrm{z}}{0-\mathrm{z}}\right)=\alpha \\
&\Rightarrow \arg \left(\frac{(\mathrm{x}-2 \mathrm{a})+\mathrm{iy}}{\mathrm{x}+\mathrm{iy}}\right)=\alpha \\
&\Rightarrow \mathrm{x}^2+\mathrm{y}^2-2 \mathrm{ax}-2 \mathrm{ay} \cot \alpha=0
\end{aligned}$
$\begin{aligned}
&\arg \left(\frac{2 \mathrm{a}-\mathrm{z}}{0-\mathrm{z}}\right)=\alpha \\
&\Rightarrow \arg \left(\frac{(\mathrm{x}-2 \mathrm{a})+\mathrm{iy}}{\mathrm{x}+\mathrm{iy}}\right)=\alpha \\
&\Rightarrow \mathrm{x}^2+\mathrm{y}^2-2 \mathrm{ax}-2 \mathrm{ay} \cot \alpha=0
\end{aligned}$

Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.