Search any question & find its solution
Question:
Answered & Verified by Expert
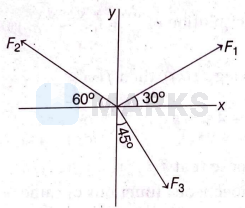
Three forces of magnitude $F_1, F_2$ and $F_3$ act on a body located at the origin as shown in the figure. The condition that gives zero net force is
Options:

Solution:
1385 Upvotes
Verified Answer
The correct answer is:
F2 = [-F1 (2 + √3)]; F3= [√6-√2]F1
Forces given are as shown

Resolving components we have,
For equilibrium ; $\Sigma F_y=0$
$F_2 \sin 60^{\circ}+F_1 \sin 30^{\circ}=F_3 \cos 45^{\circ}$
$\Rightarrow \quad F_2 \times \frac{\sqrt{3}}{2}+F_1 \times \frac{1}{2}=F_3 \times \frac{1}{\sqrt{2}}$
$\Rightarrow \quad \sqrt{3} F_2+F_1=\sqrt{2} F_3$...(i)
and $\quad \Sigma F_x=0$
$F_2 \cos 60^{\circ}=F_3 \sin 45^{\circ}+F_1 \cos 30^{\circ}$
$\Rightarrow \quad F_2 \times \frac{1}{2}=F_3 \times \frac{1}{\sqrt{2}}+F_1 \times \frac{\sqrt{3}}{2}$
$\Rightarrow \quad F_2=\sqrt{2} F_3+\sqrt{3} F_1$...(ii)
Subtracting eq. (ii) from eq. (i) we get,
$\sqrt{3} F_2+F_1-F_2=-\sqrt{3} F_1$
$\begin{array}{rrr}\Rightarrow & (\sqrt{3}-1) F_2=-F_1(1+\sqrt{3}) \\ \Rightarrow & F_2=F_1\left(\frac{1+\sqrt{3}}{1-\sqrt{3}}\right)\end{array}$
$\begin{array}{ll}\Rightarrow & F_2=-\frac{F_1(\sqrt{3}+1)^2}{(\sqrt{3}-1)(\sqrt{3}+1)} \\ \Rightarrow & F_2=\frac{-F_1(3+1+2 \sqrt{3})}{3-1}\end{array}$
or $\quad F_2=-F_1(2+\sqrt{3})$
Now, putting the value of $F_2$ in eq. (i), we get
$\begin{aligned} \sqrt{3}\left[-F_1(2+\sqrt{3})\right]+F_1 & =\sqrt{2} F_3 \\ F_1[-2 \sqrt{3}-3+1] & =\sqrt{2} F_3 \\ F_3 & =\sqrt{6}-\sqrt{2}\end{aligned}$

Resolving components we have,

For equilibrium ; $\Sigma F_y=0$
$F_2 \sin 60^{\circ}+F_1 \sin 30^{\circ}=F_3 \cos 45^{\circ}$
$\Rightarrow \quad F_2 \times \frac{\sqrt{3}}{2}+F_1 \times \frac{1}{2}=F_3 \times \frac{1}{\sqrt{2}}$
$\Rightarrow \quad \sqrt{3} F_2+F_1=\sqrt{2} F_3$...(i)
and $\quad \Sigma F_x=0$
$F_2 \cos 60^{\circ}=F_3 \sin 45^{\circ}+F_1 \cos 30^{\circ}$
$\Rightarrow \quad F_2 \times \frac{1}{2}=F_3 \times \frac{1}{\sqrt{2}}+F_1 \times \frac{\sqrt{3}}{2}$
$\Rightarrow \quad F_2=\sqrt{2} F_3+\sqrt{3} F_1$...(ii)
Subtracting eq. (ii) from eq. (i) we get,
$\sqrt{3} F_2+F_1-F_2=-\sqrt{3} F_1$
$\begin{array}{rrr}\Rightarrow & (\sqrt{3}-1) F_2=-F_1(1+\sqrt{3}) \\ \Rightarrow & F_2=F_1\left(\frac{1+\sqrt{3}}{1-\sqrt{3}}\right)\end{array}$
$\begin{array}{ll}\Rightarrow & F_2=-\frac{F_1(\sqrt{3}+1)^2}{(\sqrt{3}-1)(\sqrt{3}+1)} \\ \Rightarrow & F_2=\frac{-F_1(3+1+2 \sqrt{3})}{3-1}\end{array}$
or $\quad F_2=-F_1(2+\sqrt{3})$
Now, putting the value of $F_2$ in eq. (i), we get
$\begin{aligned} \sqrt{3}\left[-F_1(2+\sqrt{3})\right]+F_1 & =\sqrt{2} F_3 \\ F_1[-2 \sqrt{3}-3+1] & =\sqrt{2} F_3 \\ F_3 & =\sqrt{6}-\sqrt{2}\end{aligned}$
Looking for more such questions to practice?
Download the MARKS App - The ultimate prep app for IIT JEE & NEET with chapter-wise PYQs, revision notes, formula sheets, custom tests & much more.